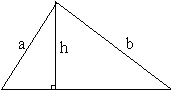
1.
(1)![]() (2)
(2)
![]()
2.
若a、b為正整數,則![]()
3.
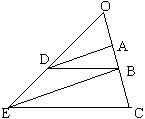
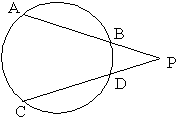
![]() 於
於![]() 上,且
上,且![]() :
:![]() :
:![]() ,則
,則![]() 坐標為
坐標為![]() 。
。
4.
設![]() 。
。
5.
聯立方程式:
![]() ,(
,(![]() )
)
(1)![]() 恰有一解。(兩直線交於一點)
恰有一解。(兩直線交於一點)
(2)![]() 無解。(兩直線平行)
無解。(兩直線平行)
(3)![]() 無限組解。(兩直線重合)
無限組解。(兩直線重合)
6.
實際值範圍:
測定值-![]() 最小測度單位
最小測度單位![]() 實際值
實際值 ![]() 測定值+
測定值+![]() 最小測度單位
最小測度單位
7.
(1)![]()
(2) 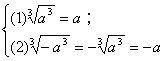
8.
(1)![]()
(2)![]()
(3)![]()
9.
(1)除法原理:![]()
(2)餘式定理:以![]() 。
。
(3)因式定理:若![]()
10.
一元二次方程式公式解:
若![]() ;且
;且![]()
則(1)D>0→二相異實解 (2)D=0→相等實解
(3)D<0→無實解
11.
根與係數:
(1)設![]() 。
。
(2)以![]()
12.
(1)若一等差數列首項![]() ,公差
,公差![]() ,則
,則![]()
(2) 等差級數:![]()
13.
(1)等比數列首項為![]() ,公比為
,公比為![]() ;則
;則![]()
(2) 等比級數※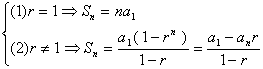
14.
(1)![]()
(2)![]() 。
。
(3)![]()
15.
(1)相對次數分配表、相對次數分配圖:
※相對次數![]()
※相對累積次數![]()
(2)算術平均數:
※未分組:總和![]() 總次數
總次數
※分組:中間值![]() 該組次數
該組次數
(3)中位數:
※奇數項:中央項
※偶數項:中央二項之平均值
(4)眾數:次數出現次數最多者(可能多解)。
16. 一元一次不等式:
※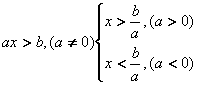
《乘除負數要變號;〝大號變小號、小號變大號〞》
17. 絕對值不等式:
若![]() ;則 (1)
;則 (1)![]()
(2)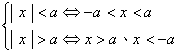
(3)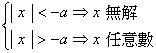
18. 以上、下判別:(+ y )

19. 以左、右判別:( + x )

20. ![]() :
:
※
21.
![]() :
:
(1)頂點![]()
(2)
(3)![]() 愈大,開口愈小。
愈大,開口愈小。
(4)交![]() 軸於
軸於![]() 。
。
(5)與![]() 軸相交情形:
軸相交情形:![]()
|
|
|
|
|
|
交點數 |
二 |
一 |
無 |
(6)兩正數和一定,則兩數相等時,其積最大;平方和最小。
21.
n邊形內角和![]() ;外角和
;外角和![]() ,對角線總數
,對角線總數![]() 。
。
※正n邊形之
|
|
21.
平行:
1、兩平行線為另一直線所截,則
(1)同位角相等。
(2)內錯角相等。
(3)同側內角互補。 ※其逆亦真!
2、平行線公式:L![]() M
M
(1)![]() (2)
(2)![]()
3、 (1)兩角之兩邊,互相平行(或垂直),則此兩角相等或互補。
(2)兩角之兩邊,一邊互相平行;另一邊互相垂直;則此二角
![]() 和
和![]() 、差
、差![]() 、和
、和![]() 。
。
23.
1、全等性質:(1) SSS (2) SAS (3) ASA (4) AAS (5) RHS
2、重要性質:
(1)垂直平分線性質:
![]() 一線段之中垂線上任一點,至此線段兩端點等距離;其逆亦真。
一線段之中垂線上任一點,至此線段兩端點等距離;其逆亦真。
(2)角平分線性質:
![]() 一角之平分線上任一點,至此角兩邊等距離;其逆亦真。
一角之平分線上任一點,至此角兩邊等距離;其逆亦真。
(3)等腰三角形性質:
![]() 等腰三角形頂角平分線垂直平分底邊,且兩底角相等;其逆亦真。
等腰三角形頂角平分線垂直平分底邊,且兩底角相等;其逆亦真。
(4)平行四邊形性質:
![]() 對邊相等、對角相等、對角線互相平分;其逆亦真。
對邊相等、對角相等、對角線互相平分;其逆亦真。
24.
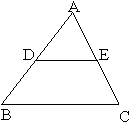
中點性質
1、一邊中點:過一邊中點且平行另一邊之直線,必過第三邊中點。
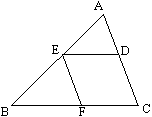
2、二邊中點:兩邊中點連線必平行第三邊且長為第三邊之半。
3、三邊中點:三邊中點連線,分原形為四全等三角形,五相似三角形;
周長為原三角形之半、面積為原三角形之1/4。
4、四邊中點:四邊中點連線,連成平行四邊形,新四邊形周長為原四邊形
對角線之和,面積為原四邊形1/2。
5、斜邊中點:斜邊中點,至三頂點等距離( R![]() )。
)。
25.
1、![]()
![]()
2、![]()
![]()
3、![]()
![]()
26.
外心角
若![]() 為
為![]() 之外心,則
之外心,則![]()
27.
外接圓半徑
(1)直角三角形:斜邊一半(![]() )。
)。
(2)正三角形:正![]() 邊長
邊長![]() ,
,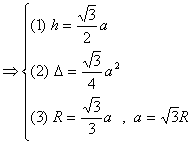
(3)一般![]() :
:
![]()
|
|
23.
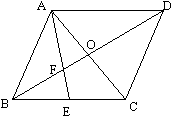
重心與中線:
若![]() 為
為![]() 之重心,
之重心,![]() 為中線,則
為中線,則
(1)![]()
(2)![]()
24.
(1)![]() 為
為![]() 之重心
之重心![]()
![]()
![]()
![]()
(2)![]() 、
、![]() 、
、![]() 為
為![]() 之三中線
之三中線![]()
![]()
![]()
![]()
![]()
![]()
25.
重心與直角三角形
若![]() 、
、![]() 分別為
分別為![]() 之外心、重心,且
之外心、重心,且![]() ,則
,則
![]()
![]()
![]()
|
|
23.
重心與平行四邊形
平行四邊形![]() ,
,![]() 中點
中點![]() ,則
,則
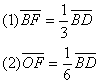
![]()
24.
(1)兩邊之和大於第三邊;兩邊之差小於第三邊。
※若![]() 為三角形之三邊長,則
為三角形之三邊長,則![]()
(2)同一三角形中
大邊對大角;小邊對小角。大角對大邊;小角對小邊。
25.
(2)中線不等式
![]() 中,
中,![]() 為中線,
為中線,
![]()
![]()
![]() ,則
,則![]()
![]()
26.
若![]() 、
、![]() 、
、![]() 分別為
分別為![]() 之中線、分角線、高,則
之中線、分角線、高,則![]()
![]()
![]()
![]()
![]() 。
。
27.
平行四邊形判別性質
(1)二雙對邊相等;
(2)二雙對角相等;
(3)二對角線互相平分;
(4)一組對邊平行且相等。
28.
菱形判別性質
(1)二對角線互相垂直平分;
(2)二對角線平分頂角;
(3)鄰邊相等之平行四邊形。
29.
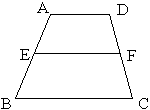
(1)梯形之中線平行上下底,長為兩底和之半。
(2)對角線中點連線平行上下底,長為兩底差之
30.
等腰梯形性質
(1)兩底角相等;兩對角線相等。
(2)若兩底角相等或兩對角線相等之梯形為等腰梯形。
(3)上底與高相等,下底與對角線相等之等腰梯形其兩底比3:5。
|
|
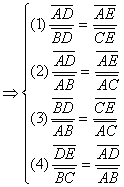
23.
1、平行線截成比例線段:
※![]()
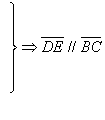
|
|
23.
![]()
|
|
23.
![]()
|
|
23.
![]()
|
|
23.
![]() ,
,![]()
![]()
|
|
|
|
23.
1、內分比
![]() 平分
平分![]()
![]()
2、外分比
![]() 平分
平分![]() 之外角
之外角
![]()
24.
(1)相似形之對應邊長比等於:
À對應高比 Á對應中線比 Â對應分角線比 Ã周長比
(2)相似形之面積比等於:
À對應高平方比
Á對應中線平方比
Â對應分角線平方比 Ã周長平方比
|
|
23.
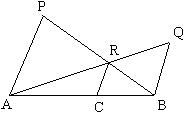
母子相似十大性質
※![]()
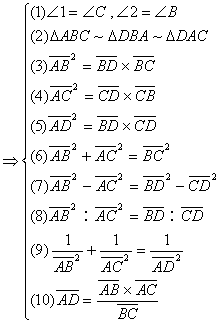
|
|
|
|
|
|
23.
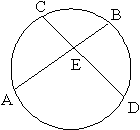
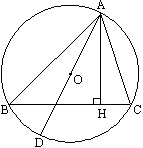
(1)內冪性質
![]()
(2)外冪性質
![]()
(3)切割線性質
![]()
(4)外接圓半徑求值公式
![]()
|
|
|
|
1. (1)倒數關係:¬![]()
![]()
![]()
![]()
![]()
![]()
®![]()
![]()
![]()
(2)商數關係:¬![]()
![]()
(3)平方關係:¬![]()
![]()
®![]()
2. 餘函數:![]()
(1)![]()
(2)![]()
(3)![]()
3.
機率:
![]() 甲事件發生的機率
甲事件發生的機率![]()
![]()